Using the Paired t-Test to compare Wegmans and Publix Supermarkets
Introduction
Waiting for Tilapia.
Waiting for Tilapia could be the title of a new indie film about the perils of climate change. But no, I was literally waiting for fish. I found myself staring aimlessly at the Tilapia in my local Publix(R) supermarket. The fresh fish is located behind a glass shield which requires a Publix employee to retrieve said fish. Don't get me wrong, I understand the need to isolate the fish from the customers. It would be undesirable to have customers squeezing and handling raw fish the same way they do oranges. My lamenting is due to the fact that I had been waiting for several minutes with no Publix employee in sight. The seafood section was unmanned and the people who are responsible for attending the seafood were cleverly located behind a door marked with the words "Publix Associates Only". After a few minutes, I gave up and opted to use chicken, instead. However, during that wait I had a great idea for this article.
While waiting, I bemoaned for the 1,000th time that we do not have Wegmans in Central Florida. If you are lucky enough to live in the vicinity of Wegmans supermarkets, then you are experiencing grocery store nirvana. I travel to upstate New York regularly and have grown accustomed to the fresh food bar, Chinese buffet, prepared vegetables and main courses, and a cheese selection that is rivaled only by a Whole Foods. In my opinion, there is a drastic difference in the selection and quality between a Publix and a Wegmans. But does this come at a cost? Does Wegmans charge more for their food to provide their superior shopping experience? Since I had recently had a question about the Paired t-Test, I decided to use the Paired t-Test to determine if Wegmans was truly more expensive.
The Paired t-Test
The Paired t-Test can be used when your data comes in logical pairs. A statistician might say that you "may be able to use a paired t-Test if you have additional information about each sample". However, that definition is unhelpful to the average practitioner, so let me clarify. The classic use of the Paired t-Test is to evaluate the before and after of some treatment. For example, measure the blood pressure of patient A, give them something (pharmaceutical, exercise, Tilapia) to reduce their blood pressure, then measure the blood pressure of patient A again. Repeat for patients B, C, D, ... In this case, the data of "Before" and "After" are paired by patient.
| Systolic Blood Pressure Readings | |||
| Patient | Before | After | |
| A | 170 | 165 | Pair #1 (Patient A Before and After) |
| B | 110 | 112 | Pair #2 (Patient B Before and After) |
| C | 134 | 131 | Pair #3 (Patient C Before and After) |
Some people might think that Patient A benefitted, as their "After" pressure is lower than "Before". Not necessarily - it is entirely possible that the "After" pressure is the result of random variation. That is, we could have done nothing and there would still be a 5 point decrease in Blood Pressure. More on this later. The Before and After example is a great way to introduce the concept of pairs; however, there are many more applications of a paired t-Test than before and after testing. Generally, you can use a Paired t-Test when the following conditions are met.
1. A data point from the first group can only be paired with a data point from the second group. Example: the 170 for Patient A "Before" should only be paired with the 165 for Patient A "After". It wouldn't be logical to pair the before data point with 112 or 131 as those were for different patients.
2. You must have exactly the same number of observations for the first and second groups. If you have 31 observations for Group A and 30 observations for Group B, that isn't close enough. It must be exactly the same. This should make sense, as there are "pairs"; if each group is a pair, how could the number of points be different?
3. If the data was taken as random samples, you can't use the Paired t-Test even if the there is a pairing factor. For example, if we measured the blood pressure of the patients two times (without giving them the medicine) then the Paired t-Test loses meaning.
Why the fuss over the Paired t-Test?
A common question is why we should use the Paired t-Test instead of the more common (unpaired) t-Test. The "normal" two sample t-Test doesn't make the assumption of pairing, so what value do we get from collecting the data in "pairs"? The statistical answer is that the Paired t-Test has more power than the normal t-Test. That is a technical way of saying that the paired t-Test can help us detect differences that the (unpaired) t-Test may miss. This is particularly true if there are outliers in the data or if the data set has a lot of variation. To help demonstrate this, I am going to use both the Paired t-Test and (unpaired) t-Test to compare the prices at Wegmans and Publix.
If you would like to know more about the (unpaired) t-Test, read this article on Roger Clemens and Barry Bonds and alleged drug use in baseball.
Step 1: Data Collection
My hypothesis is that I pay less for groceries at Publix than at Wegmans. Ideally, I would make a list of all the products I purchase at a supermarket and compare the price of each item at Wegmans and Publix. While this is theoretically possible, it would take a ridiculous amount of time. Fortunately, I can use a random sample and a Paired t-Test to answer the question in far less time.
Step 1 is to randomly select 30 products that I normally purchase at a supermarket. It is important to make these "pairs" and so care should be taken that they are identical. For example, it would be a bad idea to compare the price of 1 Gallon of orange juice at Wegmans to 1 Quart of OJ at Publix (we would expect one quart to be less expensive than one gallon). You can download the full list of products in an Excel Workbook; a sample of 5 of the 29 products is in the table below. Note: one of the products was not available at both Wegmans and Publix, so I removed that item from the list.
Price is US $ of the First Five Products out of 29 total
| Product | Wegmans Price | Publix Price | |
| skim milk, gallon | 1.89 | 3.55 | |
| Activa yogurt, plain, large | 2.69 | 2.39 | |
| eggs, large, Grade A, dozen | 1.29 | 2.69 | |
| Jif creamy peanut butter, 40 oz. | 4.39 | 5.87 | |
| Diet Coke, 12 pack | 3.33 | 4.99 |
Note: these prices are not fictional, they are actual prices taken on March 6th, 2011 from the Wegmans in Webster, NY, and subsequently March 8th, 2011 from the Publix in Windermere, FL.
Step 2: Paired t-Test
Like all hypothesis tests, the Paired t-Test starts with two hypotheses, the null and the alternate. In the case of the paired t-Test, they are based on the difference in each pair. Specifically...
H0(Null): Mean Difference (Group A - Group B) = 0
H1(Alt): Mean Difference (Group A - Group B) not equal to 0
For our specific test, we will substitute the generic terms "Group A" and "Group B" with the actual groups which are Wegmans Price and Publix Price.
H0(Null): Mean Difference (Wegmans Price - Publix Price) = 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) not equal to 0
The difference in "Mean Difference" is the delta between each pair. This is probably easier to understand by example. In the table below, the difference for each pair is in the new column entitled "Difference". For skim milk, the difference is $1.89 - $3.55 which is $-1.66. This calculation continues for all 29 rows. The average difference is then calculated for all 29 pairs. The table below only shows the first 5 pairs; click here to download the full dataset in the file Publix and Wegmans Prices for Paired t-Test.xls.
| Product | Wegmans Price | Publix Price | Difference | ||
| skim milk, gallon | 1.89 | 3.55 | -1.66 | ||
| Activa yogurt, plain, large | 2.69 | 2.39 | 0.3 | ||
| eggs, large, Grade A, dozen | 1.29 | 2.69 | -1.4 | ||
| Jif creamy peanut butter, 40 oz. | 4.39 | 5.87 | -1.48 | ||
| Diet Coke, 12 pack | 3.33 | 4.99 | -1.66 | ||
| (24 more products...) | |||||
| Average | -.809 |
Many people would stop at this point and declare that Wegmans is less expensive since the average difference is negative (remember the difference is Wegmans - Publix so a negative difference means that Wegmans is cheaper). This would be a poor conclusion. The reason we can't jump to the conclusion that Wegmans is less expensive (this is a bad time to be in your happy place) is that we have a sample, not the entire population. If I were to compare the cost of my supermarket purchases for the duration of my lifetime at Wegmans vs. Publix then I wouldn't have to worry about all this hypothesis test stuff. That, however, is outside the realm of possibilities. Therefore, I am forced to use a sample and a sample comes with error.
A wise man once said, "Given two numbers, one will be greater". Granted, there is a very small chance that the average difference would come out to be exactly zero but more likely it will be in favor of either Wegmans or Publix. What if the difference were .01 (one penny) in favor of Wegmans? Would you be quick to say that shopping at Wegmans over the long term would save you money over Publix? Perhaps Wegmans just received a large shipment of eggs and has them discounted to move them before they go bad. Perhaps if you chose a different 29 products the difference would come out as .01 in favor of Publix. Hopefully, you see that for a very small difference our confidence that Wegmans is truly cheaper could be in error.
What if the average difference over 29 products was $100 (I realize this is absurd; I am making a point). For this to happen the Wegmans price for eggs would be $1.89 and the Publix price would be $101.89 (on average). With a difference this big, we could conclude that Wegmans is less expensive with very little chance of error.
Summary so far...
If the average difference is $-0.01 we know we have a large chance of making an error if we conclude that Wegmans is less expensive.
If the average difference is $-100 we know we have little chance of making an error if we conclude that Wegmans is less expensive.
It would be nice if we could calculate the probability of making a mistake based upon the difference (and sample size). This is where the Paired t-Test comes in. It calculates a "p value" which is exactly that - it is the probability of making a mistake. Put more formally (and I am about to slip into stats speak so I don't get any nasty grams from uptight statisticians), we can calculate the probability of making a mistake if we conclude the H1 or Alternate Hypothesis. Remembering that our hypothesis table looks like this...
H0(Null): Mean Difference (Wegmans Price - Publix Price) = 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) not equal to 0
... the alternate hypothesis in plain English is "the population price of Wegmans and Publix is different". (Note to the uptight statisticians: I will discuss one-sided tests in just a second; maintain your calm.) Remember again that we have taken a sample of 29 products from my grocery list. And now we get to a key point of hypothesis testing (aka another bad time to be in your happy place).
A hypothesis test allows us to draw conclusions about the population by using a sample. For this test, the population is every product I will purchase in a supermarket over the course of my life. A sample is the 29 products that I chose from my grocery list at random. The population is almost always impossible to obtain which makes using a sample desirable. However, using a sample comes with error. First, we decide what our risk tolerance is (5% chance of making an error, 10%, etc.) and then we use the correct hypothesis test to calculate the actual amount of error.
Enough theory, let's do the math. Using Quantum XL's Paired t-Test functionality I calculated the Paired t-Test with the results below.
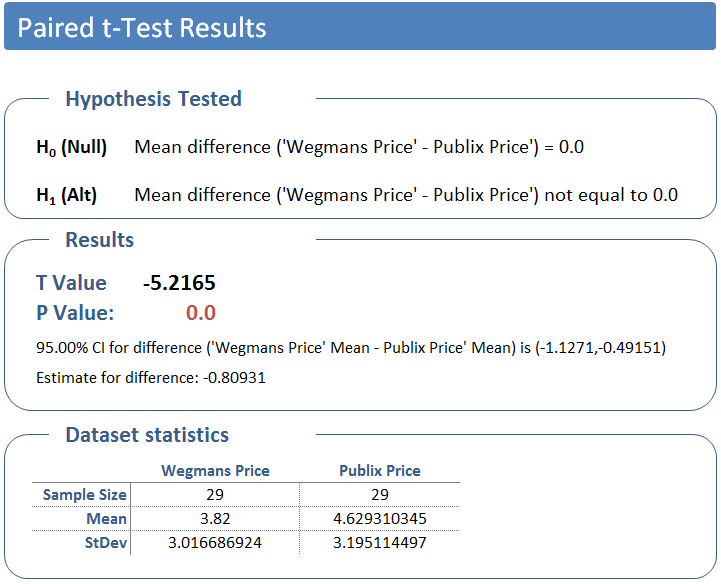
Quantum XL breaks the analysis into three sections, Hypothesis Tested, Results, and Dataset Statistics. The dataset statistics is just nice-to-have information, but the Hypothesis Tested and Results deserve special attention.
Hypothesis Tested
The Hypothesis Tested section restates the hypothesis in the event that you don't remember all the details from this article. If your datasets include titles (i.e., the words "Wegmans" and "Publix") then the hypothesis will be stated in those terms. I highly recommend using titles as it simplifies later interpretation. Once more, the null hypothesis is the mean difference is zero; the alternate is the mean difference is not zero.
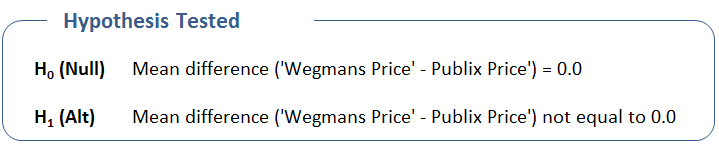
Results
The Results section has "the answer" or our P Value, our probability of making a mistake if we conclude the price difference is not zero. In our case, the P value is so close to zero that Excel rounds it to zero.
In actuality, the probability of making a mistake can never truly be zero; Excel is rounding the results. I reformatted the results and displayed the P Value to more digits with the result below. If we conclude that the population prices are different, then we only have a .0000153 (or .00153%) chance of making a mistake. To put this in perspective, we have 15 chances out of a million of making a mistake. Note: the T Value is a bit geeky, and unless you want to understand the math behind this test, we don't need to use it.
Below the P Value is some supporting information. Since we know that the difference is likely not zero, then what is it? Well, in this case we can be 95% confident that the difference is between $-1.13 and $-.49, with the estimated difference equal to $-0.81. Or, put more simply, Wegmans is less expensive by $.49 to $1.13.
How do I state the results?
If you remember, this started when I was waiting for Tilapia in my local Publix. I hypothesized that Wegmans must charge more for their superior shopping experience (in my opinion). I established my hypothesis and then collected my sample. Side note: I almost fell out of my chair when I saw that Wegmans was less expensive than Publix for these 29 items. However, I can continue my analysis to determine if this is random variation or a real difference. Using the sample, I calculated the P Value at .0000153. At this point, I must be careful about what this means. So let's go through a few options of how to state this.
Method 1: The uptight stats Nazi method. If you read medical journals for entertainment you may see similar statements.
I choose to reject the null hypothesis and conclude the alternate. There is .00153% chance that this is an error, which is below my previously stated threshold of risk of 5%.
Method 2: More friendly but still correct method
Based upon our sample of 29 products, we can conclude that the prices of Wegmans and Publix are different with a chance of error equal to .000015.
Method 3: Easiest to understand (caution: may make uptight statisticians squirm)
Based upon my sample of 29 products, I am 99.99846% confident that the prices at Wegmans and Publix are different.
The reason Method 3 causes pause is due to the swap from "probability of an error" to "percent confidence". Personally, I use this method as more people can relate to this interpretation than the other two.
Finally, I should note a common mistake that is wrong, and not just to the uptight stats Nazis.
Method 4: Commonly stated but incorrect
There is a .00153% chance that the means are equal.
What I just changed was subtle so let me ensure you caught it. Instead of expressing the percent error as "not equal" (which is the H1 or alternate hypothesis) I switched to "equal" which is the H0 or null hypothesis. We should not do this. It is one thing to calculate the probability that two means are not equal, but we can't really talk about equality. Why? Well, that is a somewhat hard concept and one of the most confusing parts of a hypothesis test. We can find evidence that the means are not normal, and express confidence that the means are not normal, but this is not the same as evidence that the means are normal.
Comparison of Paired t-Test to "Normal" or Unpaired t-Test
Quantum XL also includes a normal or unpaired t-Test. Most software will usually call this a Two Sample t-Test or simply t-Test (if no reference to pairing is made it is assumed unpaired). If I run the unpaired t-Test on this dataset, the results are below.
Note that the P Value is much larger than in the paired t-Test. If I conclude they are different, I have a 32.56% chance of an error (1 in 3). For most experimenters, this is too great a chance of error and they will state they failed to find a difference in the means. Note that the conclusions are opposite based on which test I perform.
If I use the Paired t-Test, I conclude that mean prices are different.
If I use the (Unpaired) t-Test, I fail to find a difference in means.
Why is the t-Test result so much different? I am going to slip into some geeky math speak for just a second. If you aren't interested or are barely hanging on, simply remember that you should use the Paired t-Test if your data is in pairs and skip to the next section. If you like the geeky stuff, read on. For this dataset the answer is in the variation. Since the prices of the individual products are so varied, this shows up in the t-Test as noise. The t-Test is based on the T Value which is essentially a Signal to Noise ratio. More formally, the math for the t-Test is below.
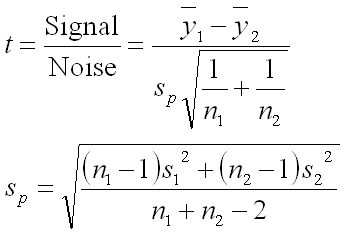
As the Noise increases, the T Value will go down. The result is a smaller T Value and a larger P Value. For more information about the math behind the (unpaired) t-Test, it is fully explained in the article Calculating Type I Probability using the Roger Clemens dataset as an example. When we use the Paired t-Test, the difference between prices in products is removed, thus greatly reducing the noise. The differences are being compared and variation between products is not considered.
Single-Sided Test
Earlier in the article I indicated that I would appease the uptight stats Nazis with a single-sided test discussion. The concept of a single-sided test is really quite trivial. Instead of the null hypothesis being equality, it is less than or equal to some number, usually zero. Below is the formal definition of a two-sided vs. one-sided test with the key differences in bold.
Two-sided test
H0(Null): Mean Difference (Wegmans Price - Publix Price) = 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) not equal to 0
One-sided test Method 1 (Is Publix Less Expensive)
H0(Null): Mean Difference (Wegmans Price - Publix Price) <= 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) > 0
One-sided test Method 2 (Is Wegmans Less Expensive)
H0(Null): Mean Difference (Wegmans Price - Publix Price) >= 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) < 0
While the two-sided test intends to answer the question "are the prices different", the one-sided test is closer to our original inquiry "Is Publix less expensive?". Using a one-sided test is not without controversy, but let me explain that at the end.
Quantum XL's hypothesis tests include options to run either a one-sided or two-sided test. If I run the test for the original hypothesis (aka "Is Publix Cheaper") then I would run the One sided test Method 1. The formal statement of the hypothesis and the result is below.
One-sided test Method 1 (Is Publix Less Expensive)
H0(Null): Mean Difference (Wegmans Price - Publix Price) <= 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) > 0
The P Value comes out to .99999233, and that means that if we conclude that Publix is less expensive then we run a 99.9999233% chance of making a mistake. This is not a good bet. In fact, running this test at all was folly since the sample data shows a price advantage for Wegmans. So let's look at one-sided Method 2 (Is Wegmans Less Expensive).
One-sided test Method 2 (Is Wegmans Less Expensive)
H0(Null): Mean Difference (Wegmans Price - Publix Price) >= 0
H1(Alt): Mean Difference (Wegmans Price - Publix Price) < 0
That is more like it. Our P Value indicates that if we conclude that Wegmans is less expensive, then we have a .000767% chance of making a mistake. Don't you wish you could get those odds at Vegas.
And now the controversy. The one-sided (sometimes called single-sided) test, for most hypothesis tests, returns a P Value that is half that of the two sided test. In this example, the two-sided test resulted in a P Value = .0000153; the one sided was exactly half of that value. So why is this a concern? A lot of people run their hypothesis test in this manner...
1. Collect data on Wegmans vs. Publix.
2. Calculate mean difference and note that for sample Wegmans is less expensive.
3. Pose hypothesis "Is the Population of prices at Wegmans less expensive than Publix?"
4. Use Quantum XL's Paired t-Test to generate P Value.
5. If P Value is less than .05, then conclude that Wegmans is less expensive; if not, then conclude that you don't know.
This flow seems like it is OK but it really isn't. The reason is that you looked at the data in step two, before you formed your hypothesis in step three. This is kind of a statistical nit, but if you think about it, you can always reduce your P Value in half as you will always know which sample has a smaller mean difference.
The correct flow is something like this...
1. Pose Hypothesis "Is Publix less expensive than Wegmans" and establish a criterion value for acceptance of the alternate (usually .05).
2. Collect sample data.
3. Use Quantum XL's Paired t-Test to generate P Value.
4. If P Value is less than .05, then conclude that Publix is less expensive; if not, then conclude that you don't have enough evidence.
Note that we formed the hypothesis first. The fancy phrase "establish a criterion value" in step one simply means you decide before you run the test how much risk you are willing to take. The most common value is .05. How do you use it? Let's say you do the test and the P Value comes out to be less than .05; you should then accept the alternate hypothesis. However, if it comes out to be greater than .05 then you must reject the alternate hypothesis and accept the null. That means that if it comes out to be .05001 you should reject the alternate. Do most people do this? Frankly, no (not even the uptight statisticians).
Final Discussion
The Paired t-Test is an excellent tool when its use is appropriate. If the data is logically grouped in pairs, the Paired t-Test is more powerful than the (unpaired) t-Test.
Based upon my sample, my original hypothesis was wrong. Publix is not less expensive. Quite the opposite, in fact. For the products I purchase I am very confident that Wegmans is less expensive. I am now in a bit of a conundrum: how can Wegmans afford to provide the much higher quality experience (again, in my opinion) as compared to Publix? I don't have an answer to that, but I plan on asking Wegmans the next time I am there.
Disclosure and Disclaimer
I am not affiliated with either the Wegmans or Publix company. I have not been paid by either party and have never worked with either company.
This analysis was specific to my shopping habits. I didn't choose 30 products at random, I chose 30 products at random from my shopping list. Why? My goal was to see if I would benefit from shopping at Wegmans (not the average consumer). A different sample from another shopping list may result in a different answer.
According to Wikipedia, Wegmans is privately owned with Danny Wegman serving as the CEO. Danny, if you are reading this please, I am begging you, extend your chain of supermarkets to Central Florida, I am tired of waiting for overpriced Tilapia.
I intended to post some pictures with the article; however, the Wegmans Consumer Affairs department would not allow pictures to be taken from within the store. This is the one head scratcher in mostly good experiences with Wegmans. It's not like they are designing stealth bombers; what about cheese and produce displays could be a secret? Perhaps their Tilapia are working with the CIA. The Wegmans Consumer Affairs also declined an interview and comment.
Corrections and Additions
March 22, 2011 - A reader pointed out that the sign on the door next to the seafood department has the words "Publix Associates Only" and not "Employees Only".
March 22, 2011 - I have had numerous readers inquire which Publix in Windermere was referenced in the article. To my knowledge there are only two Publix in Windermere. One is by Isleworth and is a aptly named "Cascades at Isleworth". That is not the Publix in this article. I was shopping in the Publix located near Summerport village and I believe it is called "Cornerstone at Summerport". It is located just off highway 535.
March 22, 2011 - As of this update, Publix has not responded to our request for comment.
March 28, 2011 - Correction to the spelling of Danny Wegman's name.
leave us a comment
