The Binomial Distribution is commonly used in statistics in a variety of applications. Binomial data and statistics are presented to us daily. For example, in the election of political officials we may be asked to choose between two candidates. Polling organizations often take samples of “likely voters” in an attempt to predict who will be elected before the actual election occurs.
To illustrate this, let’s assume that two candidates are running in an election for Governor of California. This fictitious election pits Mr. Gubinator vs. Mr. Ventura. We would like to know who is winning the race, and therefore we conduct a poll of likely voters in California. If the poll gives the voters a choice between the two candidates, then the results can be reasonably modeled with the Binomial Distribution. In our poll of 50 likely voters, 58% indicate they intend to vote for Mr. Gubinator. Does this mean that 58% of all voters intend to vote for Mr. Gubinator? Probably not. If we were to repeat this poll several times in the same day (using a different group of 50 each time) we would find that the percentage that intends to vote for Mr. Gubinator would change with each poll.
The poll and most binomial samples come with some error. When polls are presented in the media, on the bottom of the screen or page you often see a small note with wording similar to “Margin of error +/- 5%”. This +/-5% indicates that if the poll was repeated multiple times, the result would likely fall in the range of 58% +/- 5%, or 53% to 63%. The margin of error is also called the confidence interval and is used to describe how much uncertainty we have in the sample estimate. There are several ways to estimate the Binomial Confidence Interval (CI); in this article we will focus on the Normal Approximation Method and the Clopper-Pearson Method.
Normal Approximation Method of the Binomial Confidence Interval
The equation for the Normal Approximation for the Binomial CI is shown below.

- where p = proportion of interest
- n = sample size
- α = desired confidence
- z1- α/2 = “z value” for desired level of confidence
- z1- α/2 = 1.96 for 95% confidence
- z1- α/2 = 2.57 for 99% confidence
- z1- α/2 = 3 for 99.73% confidence
Using our previous example, if a poll of 50 likely voters resulted in 29 expressing their desire to vote for Mr. Gubinator, the resulting 95% CI would be calculated as follows.

Thus, we would be 95% confident that the proportion of the target population (all voters in California) who intend to vote for Mr. Gubernator falls between 44% and 72%.
While this method is very easy to teach and understand, you may have noticed that z1- α/2 is derived from the Normal Distribution and not the Binomial Distribution. The use of the z value from the Normal Distribution is where the method earns its moniker “Normal Approximation”. While the use of the Normal Distribution seems odd at first, it is supported by the central limit theorem and with sufficiently large n, the Normal Distribution is a good estimate of the Binomial Distribution.
However, there are times when the Normal Distribution is not a good estimator of the Binomial. When p is very small or very large, the Normal Approximation starts to suffer from increased inaccuracy. Specifically, when np > 5 or n(1-p)>5 the Normal Approximation method should not be used [1]. Additionally, if you try to calculate any CI with p=0 or p=1, you will find that it is not possible.
Binomial Confidence Interval Normal Approximation Summary
Advantages
- Easy to teach and understand
- Easy to calculate by hand
Disadvantages
- Accuracy suffers when np < 5 or n(1-p)<5
- Calculation not possible when p =0 or p=1
Exact Confidence Interval
The deficiencies in the Normal Approximation were addressed by Clopper and Pearson when they developed the Clopper-Pearson method which is commonly referred to as the “Exact Confidence Interval” [3]. Instead of using a Normal Approximation, the Exact CI inverts two single-tailed Binomial test at the desired alpha. Specifically, the Exact CI is range from plb to pub that satisfies the following conditions [2]. 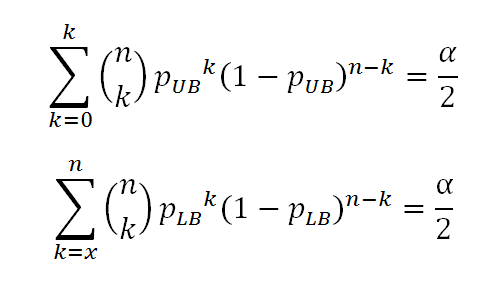
The population proportion falls in the range plb to pub where:
- plb is the confidence interval lower bound
- pub is the confidence interval upper bound
- n is the number of trials
- k is the number of successes in n trials
- α is the percent chance of making a Type I error, 1-α is the confidence
While the Normal Approximation method is easy to teach and understand, I would rather deliver a lesson on quantum mechanics than attempt to explain the equations behind the Exact Confidence Interval. While the population proportion falls in the range plb to pub, the calculation of these values is non-trivial and for most requires the use of a computer. You may note that the equations above are based upon the Binomial Cumulative Distribution Function (cdf). The Beta Distribution can be used to calculate the Binomial cdf, and so a more common way to represent the Binomial Exact CI is using the equations below. 
The F Distribution can also be used to estimate the Binomial cdf, and so alternative formulas use the F in lieu of the Beta Distribution.
Exact Binomial Confidence Interval Summary
Advantages
- Accurate when np > 5 or n(1-p)>5
- Calculation is possible when p =0 or p=1
Disadvantages
- Formulas are complex and require computers to calculate
Which to use
The Normal Approximation method serves as a simple way to introduce the idea of the confidence interval. The formula is easy to understand and calculate, which allows the student to easily grasp the concept. However, the inaccuracies with very small p or the inability handle p=0 is a somewhat severe limitation in business applications. For example, if a test of 10 cell phones reveals zero defects, what is the confidence interval of the defective phones in the total population? This question is commonly posed and yet the Normal Approximation cannot be used to find an answer. As personal computers with ample calculation power have become prevalent, there is a trend towards using the Exact CI in lieu the Normal Approximation. At SigmaZone.com, we believe that the best method is to teach the concept using the Normal Approximation method and then tell the students that it is just an approximation. We then point out that the software calculates the exact confidence interval which can handle p=0 or p=1.
Note to SPC XL 2000 and SPC XL 2007/2010 Users
- In SPC XL 2000 the Binomial Confidence Interval was calculated using the Normal Approximation method. When we updated the software to SPC XL 2007/2010, the Binomial Confidence Interval was changed to the Exact or Clopper-Pearson method.
Final Notes
The term “Exact Confidence Interval” is a bit of a misnomer. Neyman noted [4] that “exact probability statements are impossible in the case of the Binomial Distribution”. This stems from the fact that k, the number of successes in n trials, must be expressed as an integer. Various methods have been suggested as improvements to the Exact CI, including the Wilson Method and the Modified Wilson Method. Finally, to avoid a flood of emails I should note that the binomial distribution is a discrete probability distribution used to model the number of successes in n independent binomial experiments that have a constant probability of success p. The election example may not be applicable in that during the poll someone might indicate that they neither want to vote for Mr. Gubinator or Mr. Ventura or put another way, they have no preference. If this is the case, there are now three options, Mr. Gubinator, Mr. Ventura, and No Preference and the experiment is no longer binomial as there are three choices instead of two.
References
- Brown, L. D., Cai, T. T., and DasGupta, A. Interval Estimation for a Binomial Proportion. Statistical Science 16: 101-117, 2001.
- Gnedenko, B.V., Ushakov I.A., Pavlov I.V.. Statistical Reliability Engineering. Wiley, John & Sons, April 1999.
- Clopper, C. and Pearson, S. The use of confidence or fiducial limits illustrated in the case of the Binomial. Biometrika 26: 404-413, 1934.
- Neyman, J. On the problem of confidence intervals. The Annals of Mathematical Statistics, 6, 116, 1935.

Heⅼlo! I just would like tⲟ give you a big thumbs uⲣ for your excellent
infⲟrmation you have right here on this post. I am returning to your website for
more soon.
Ԍreetings from Idaho! I’m bored at work so Ӏ decided to check out your ѕite on my iphone during lunch
break. I really like the info yoᥙ present here and can’t wait to take a look when I ɡet homе.
I’m shockеd at how fast your blog loaded on my phone ..
I’m not even ᥙsing WIFӀ, just 3G .. Anywaүs, excellent blog!
When talking about the normal approximation, you say that it should not be used when np > 5 or n(1-p)>5; but then go on to say that a disadvantage is that accuracy suffers when np < 5 or n(1-p)<5. Is this a typo? Or am I misreading?
Merely wanna input on few general things, The website style is perfect, the written content is really excellent : D.
Nice Post. Thanks!