Most practitioners who use hypothesis test use the t-Test and F-Test to determine differences in mean and variation respectively. If you are new to hypothesis testing, try the introductory article on the alleged use of performance enhancing drugs by Roger Clemens and Barry Bonds.
Not all datasets are appropriate for the t/F Test. To illustrate this, I will compare the load times of two different hosting companies, Alentus and HostMonster. If you are interested in my motivation, read the full back story or if you are only interested in the math skip it. The short version …. I am comparing the page load speed of my current host, Alentus, to another hosting company, HostMonster. I should note that this isn’t a fair comparison since Alentus costs $21.95 per month and HostMonster costs $5.95 per month; however, the statistics are still valid and the final results were completely unexpected.
After collecting the data, I intended to use the t/F Test to compare the two datasets. Unfortunately, the load times were highly skewed. Both the t-Test and the F-test make an underlying assumption of normality. Below is a dot plot from Quantum XL for the load times from the pages hosted by Alentus. You can download an Excel Workbook with the full dataset by clicking here.

The X Axis is the load times of each page measure in Seconds. The load time is usually very small, 2 or 3 seconds, but there are several observations well in excess of 100 seconds and two greater than 400 seconds. This data is highly skewed so a visual inspection of the data appears non-normal. A formal measurement of normality is the Anderson Darling test. I ran the Anderson Darling test on the Alentus data set with the results below. Note that the p-value is less than .005, indicating that we are greater than 99.5% confident that the data is not normal.
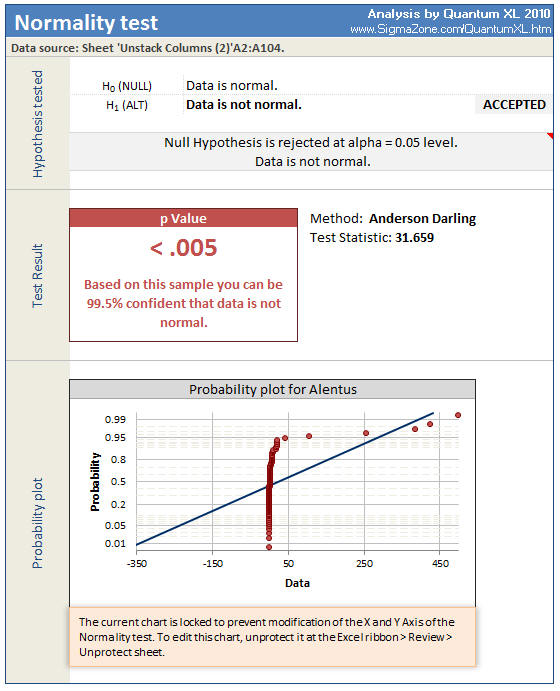
Thus, our assumption of normality is violated and we should no longer use the t-Test or F-Test. Understanding which test to use instead of the t/F Test is an important aspect of statistics and should not be ignored. If you always use the t-Test to determine a difference in location, then you are likely making a significant mistake.
The t-Test is a hypothesis test for the mean and as such falls into a more general category of hypothesis tests for location. The F-Test is a hypothesis test for variation and falls into the category of measure of dispersion or spread. The result of a hypothesis test for variation can affect which test we use for location, so we shall begin with testing for variation.
Hypothesis Test for Variation
Selecting the correct hypothesis test for variation is relatively simple. We need only to know if the data is normal and if there are two or more samples (or data sets). In the above example, there are only two samples, Alentus and Host Monster. The flow chart below is a map to the correct test. The first step is a determination of normality. There are many different tests for normality, such as Kolmogorov Smirnov, Shapiro Wilk, and Anderson Darling. I chose to use the Anderson Darling (AD) test for this dataset. As mentioned before, the AD test rejected normality so we must follow the flow chart to Levene’s Test.

The result of Levene’s Test is below.
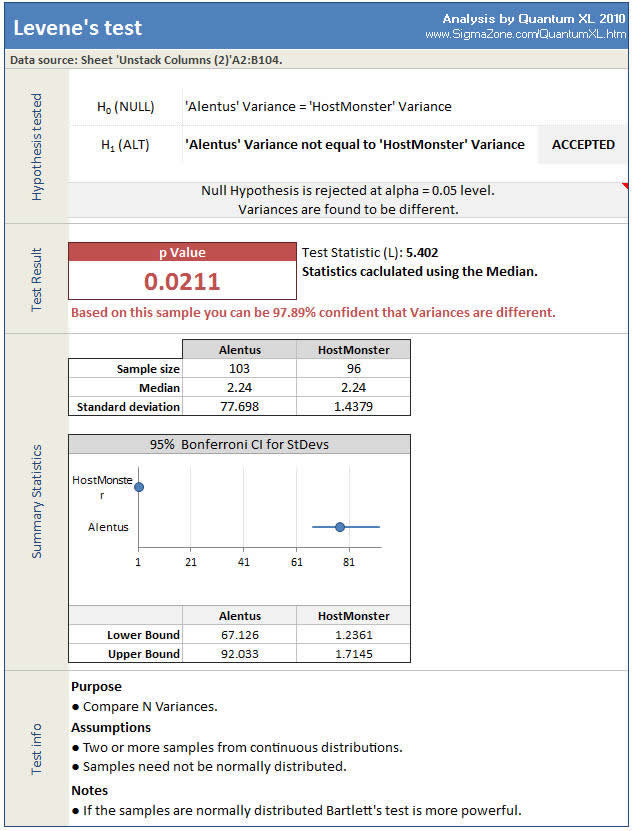
Levene’s Test returns a p-value of .0211, which indicates that we can be 97.89% confident there is a difference in variation. Quantum XL displays the assumptions for each hypothesis test at the bottom of the analysis. This is a convenient reminder to help prevent errors.
Hypothesis Test for Location (Mean/Median)
Hypothesis testing for the mean is a little more complex than for the variation. The factors that affect the correct test to run are…
Normality – Are the samples normally distributed or some other distribution?
Number of Samples or Data Sets – Can be 1 sample, 2 sample, or more than two samples. An example of one sample would be to compare the mean of a single sample to a hypothesized value. For example, we could test the hypothesis that Alentus’ page load time (just Alentus, not including HostMonster) is 2 seconds. An example of a two sample test is a comparison of Alentus’ mean to Host Monster’s mean. Finally, more than two samples would be a comparison of Alentus, HostMonster, and some other company.
Paired Data vs. Unpaired Data – Does the data fall into logical pairs? For more information read this article on the paired t Test.
Equal Variances – Are the variances of each sample the same? This only applies to tests with 2 or more samples. Since we need to know this for hypothesis test for location, we typically perform a variance test first.
Symmetrical or Skewed – Are the samples symmetrical or skewed? An example of a symmetrical distribution is the Normal distribution. The left side looks like the right side. It is possible to have a non-Normal distribution that is symmetrical.
Outliers – Do the samples include outliers?
Including a single flow chart for all the options didn’t fit on a single web page easily. Therefore, there are two flow charts below, one for Normally Distributed data and the other for Non-Normal data.
Hypothesis Test For the Mean (Normally Distributed Data)
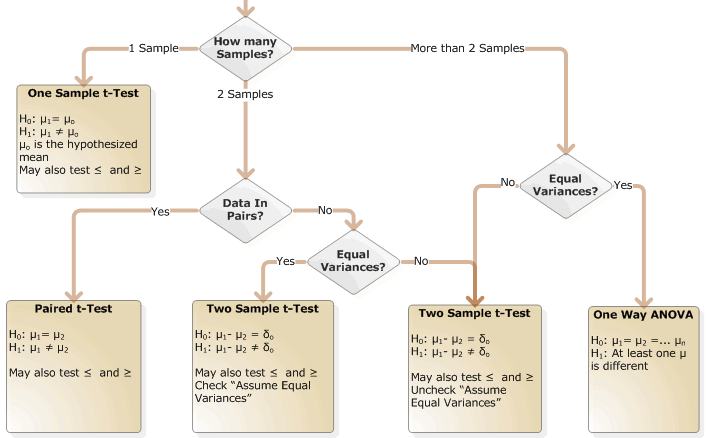
Hypothesis Test For The Median (Non-normal Data)

For the comparison of Alentus vs. HostMonster, we have already established that the data is not normal. We have two samples (Alentus and HostMonster) so we proceed down the path that asks about “Matched Samples”. The concept of Matched Samples is similar to a paired t-Test, but is beyond the scope of this article. The next step is “Equal Variances”. We have already run Levene’s test and have established that the variances are not equal. Therefore, we follow the flow chart to “Outliers”. The dot plot seemed to indicate that we have outliers; however, a box plot makes the identification much easier.
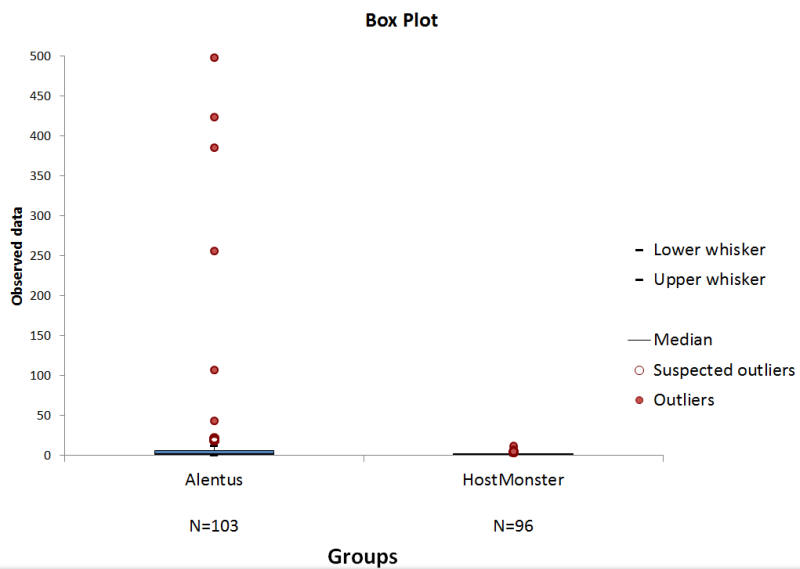
For those of you familiar with a Box Plot, you might wonder why this one looks so odd. The boxes are so small at the bottom of the chart, they almost look like little blue lines. The red dots above the boxes are the suspected outliers and outliers. Since the Box plot identified several points within the Alentus dataset as outliers, we should proceed down the flow chart to Mood’s Median. The results of the Mood’s Median test are below.
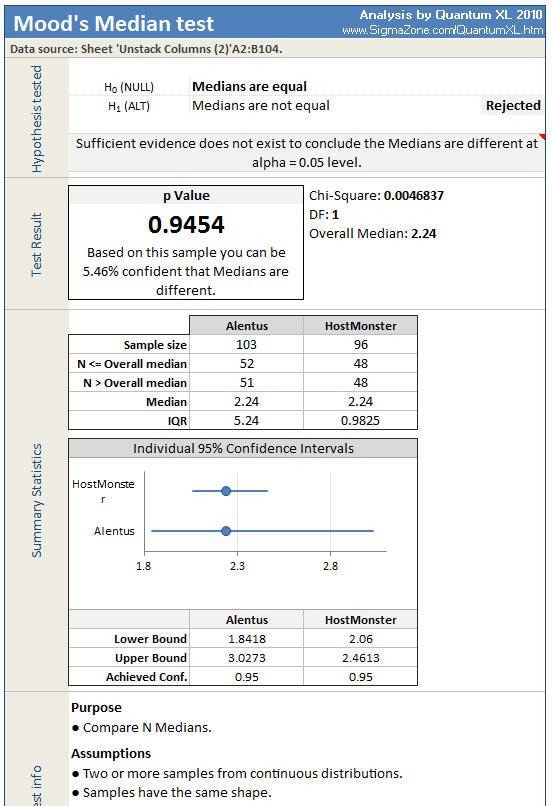
The median of both data sets is 2.24, so it shouldn’t be a surprise that the Mood’s Median fails to detect a difference in median.
Final Conclusions
If you remember, my ultimate goal was to learn if I should act or not. My assumption going into the test was that Alentus would be as fast as, and likely faster than, HostMonster. The foundation of this hypothesis was that Alentus is 4 times as expensive. However, the actual testing did not meet with my expectations. The median load times for the two are nearly identical. However, the variance is not. When our customers come to our site hosted on Alentus, some wait for a very long time. As a result, I decided to act. I changed hosting providers shortly after collecting the data.
The F-Test and t-Test are not a universal solution. Various factors, such as Normality, skew, outliers, and equal variance affect which hypothesis test is appropriate in each situation. Download this pdf which can assist you in selecting the correct hypothesis test.
Quantum XL’s AutoTest
For those of you who have a hands off approach, Quantum XL includes a new feature called “AutoTest”. When you use AutoTest, Quantum XL implements the flow chart to determine the correct hypothesis test to run for a set of data. Download an Excel workbook with the AutoTest for this article.
