Deflategate has been in the news extensively in the past few months. The Ted Wells report includes 139 pages of text messages, rules, and data which delves into the hypothesis that the Patriots were responsible for deflating their footballs. Attached to the report is a 68 page lab analysis which is used to support the hypothesis.
According to the Wells report, “Rule 2 of the Official Playing Rules of the NFL requires footballs used during NFL games must be inflated to between 12.5 and 13.5 psi.” Does the NFL’s measurement system have the precision required to measure footballs in this range?
Measurement System Used by the NFL
The Wells report tells us that the NFL measures the footballs before each game (page 7). On the day of the game, one official measured all of the balls. At halftime, at the request of the Colts, 15 balls were measured again by two different officials using two different gages (page 7,8).
In terms of a Measurement System Analysis (MSA), each of those 15 footballs is a “part”. The officials measuring the footballs with the gage are “Appraisers” or sometimes “Operators”. The requirement for the football to be between 12.5 and 13.5 psi sets the specification (spec) limits. Specifically, the Lower Spec Limit (LSL) = 12.5 and the Upper Spec Limit (USL) = 13.5.
The data in MSA form is below. Parts 1 through 11 are the footballs from the Patriots and Parts 12 through 15 are footballs from the Colts.
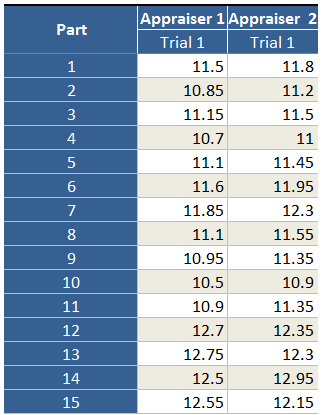
Since two officials measured the same football, this gives us the rare ability to calculate the measurement variation (sometimes called Gage R&R) for the NFL’s measurement process.
In this article, I use the equations for MSA as established by the Automotive Industry Action Group (AIAG).
Typically, an MSA is used to answer two basic questions…
- Can the measurement device determine if a part (football) is between the spec limits?
- How much of the total variation in measurements is coming from the measurement system vs. the parts?
In this example, the first question is interesting but the second is not. If you’d like to know why the second question isn’t interesting, I’ve put an explanation at the end of the article.
MSA Results
The results of the ANOVA method (see AIAG MSA revision 4) of performing an MSA are below. Note that the “Total Gage R&R” row reflects the amount of variation in the measurement system. Specifically for this dataset, the standard deviation of the measurement system is .27598 or approximately .3. The interpretation of a sigma measure = .3 is quite simple… 99.73% of measurements of the same football will fall in the range of +/- 3*sigma measure or in this case +/- .9 psi.
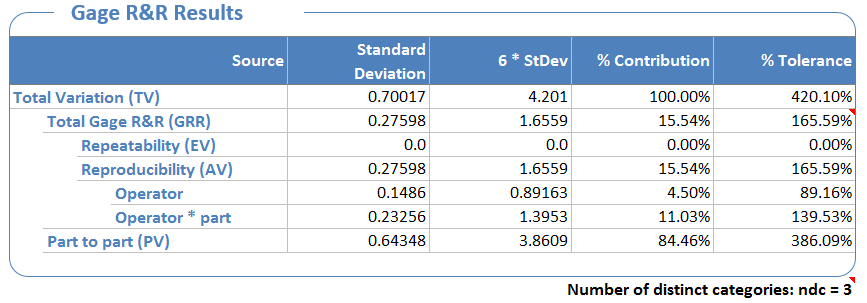
Since the spec limits are 1 psi wide (13.5-12.5 = 1) the measurement variation exceeds that of the spec limits. Put another way, the spec limits are 13 +/- .5. The measurement system can be off by +/- .9. The variation in the measurement system is greater than that of the spec limits.
If you were to provide this measurement system with a football that had a true pressure = 13 psi, it could easily measure that football less than 12.5 or greater than 13.5. This is an indication of not just a poor, but atrocious measurement system.
Graphical Results
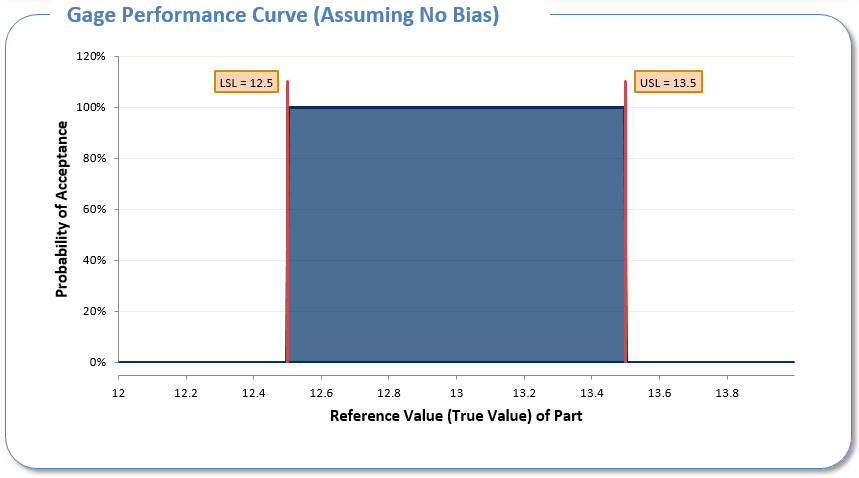
The ratio of the measurement variation to the spec limits can easily be seen by the gage capability curve below. The x axis is the “true value” of a football. The “true value” represents the measurement of pressure as if there were no measurement variation. The vertical axis is the probability of acceptance or in this case the probability that the referee would accept that the football is between 12.5 and 13.5.
Below is an example of a perfect measurement system, one that has no measurement variation. Note that when the true value is between 12.5 and 13.5, there is a 100% chance of the referee accepting the football. However, when the true value is less than 12.5 or greater than 13.5, there is a 0% chance of acceptance.
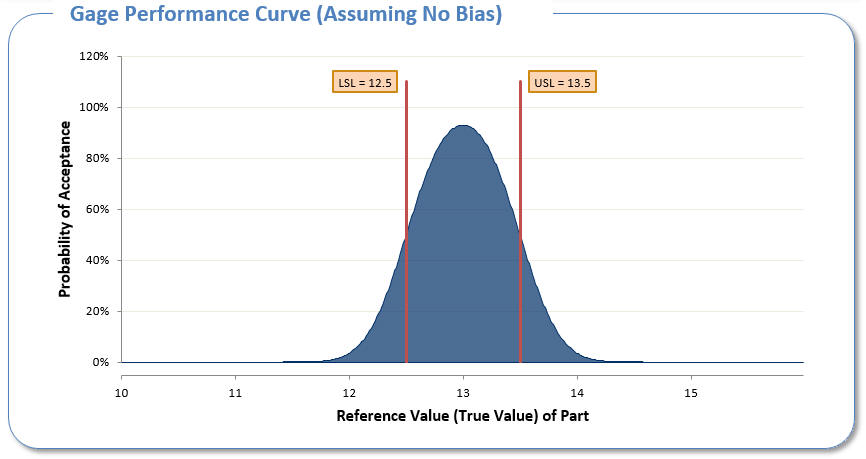
The curve above is for a perfect gage. The curve below is the gage capability curve for the football measurements provided by the Wells report. Note that in the best case scenario, when pressure = 13, there isn’t a 100% chance of acceptance. As the true value gets closer to the spec limits, the probability of accepting a football drops quickly.
Conclusions
The NFL’s rules require that a football be between 12.5 and 13.5 psi. Using the data provided by the Wells report, the NFL’s current process is not adequate to make that determination. My conclusion is at odds with those from the Wells report. The primary problem in the Wells report is the assumption that five individual operators would perform the same as the referees on game day.
Metaphorically, this is analogous to a student (referee) failing an exam at school. The parents (NFL), in an attempt to evaluate the student, hire someone else to take the exam (Wells and the five individual operators), who subsequently pass. Thus, the parents conclude that the student was capable the entire time.
Notes
Given the emotional nature of the subject, there are likely going to be numerous objections to this article. Before leaving an inflammatory comment, please read the following notes.
The Wells report includes its own evaluation of the measurement system, specifically on page 26 of the attachment from the independent lab, in a section entitled “The Effect of Human Factors on Gauge Accuracy”. In this section, they selected “five individuals” to make measurements. From these five individuals, they concluded that “the measurements on Game Day were unlikely to have been affected by issues relating the human factors”. This analysis makes the dubious assumption that the five individuals would have similar measurement variation as the NFL’s referees on game day. For the actual measurements, the NFL referees were different humans, received different training, and took the measurements under different conditions. Specifically, the report mentions that the referees only measured 4 Colts balls since they ran out of time at halftime. Given that the actual data from the measurements taken by the actual NFL referees was available, it seems odd that the report would conclude that operator variation was small when the data would indicate that it was actually quite large. Perhaps they considered the sample size inadequate (see notes below).
Measurement variation can be caused from the actual gage (i.e., the pressure gage) and the human using the gage (operator variation). From my analysis, we can’t tell which is the source of the variation. However, that isn’t relevant since the “measurement system” includes both human and gage variation.
Ideally, an MSA would be conducted where each appraiser took multiple measurements of the same part. The NFL data didn’t include this component of variation. In terms of an MSA, this is called “repeatability”. This component of variation can’t be estimated from the data. Thus, this analysis assumes that repeatability = 0; however, if it were included the variation would likely increase, making the NFL’s measurement system even worse.
The sample size for this measurement analysis is not as large as is typical for an MSA. With a larger sample size the estimated measurement variation could increase or decrease.
This analysis assumes that the measurement system is “unbiased” or that the measurement system is correct on average (i.e., multiple readings have variation but their average is the true value). This is a poor assumption; however, if the measurement system did have bias, it would make the misclassification of footballs even higher.
The method of analysis is the ANOVA method of MSA in accordance with AIAG’s calculations in the 4th edition of their MSA book. Many people might wonder why I used the AIAG standard for MSA. Since the automotive industry is so large, many companies use AIAG as a standard even if they are not in the automotive industry.
There are other methods to calculate the statistics, including the XbarR method. It produces similar results to the ANOVA method.
For those of you familiar with MSA, I didn’t comment on the ratio of measurement variation to part variation. The %GRR is 39.42%, which exceeds AIAG’s rule of thumb of 30%. However, the variation in the footballs (part/product variation) isn’t under the control of the NFL. Each team inflates/deflates its own footballs. Thus, each team is likely to have its own part variation. This analysis included parts from two different teams, which would likely inflate sigma product. As product variation is outside the NFL’s control, it would be unfair to criticize their ratio of sigma measure to sigma product. However, none of this changes the ratio of sigma measure to the spec range.
This analysis is completely centered around the ability of the NFL to measure footballs between 12.5 and 13.5 psi. The existence of a mean shift from before the game to halftime is not addressed. The potential mean shift between Colts’ and Patriots’ footballs is also not addressed.
My primary area of concern with regard to the report’s lab results centers around the impact of human variation of which a concern is the Hawthorne Effect. The Hawthorne Effect simply states that an individual gives more attention to what they are doing if they are being observed. The “five individuals” who they used to mimic the referees likely already knew about Deflategate, knew that their results would be in the report, and gave much more attention to the measurements than the NFL referees did. Of course, I can’t say with 100% certainty that this is the case; however, the data from the referees is a representative sample from the actual process and doesn’t make this assumption.
I’ve been asked by the engineers and scientists I work with about the guilt and innocence of the Patriots. The Patriots balls measured far less than the required 12.5 psi; even by my analysis, it is unlikely that these balls were in spec. However, what my analysis can’t account for is overall system bias. Bias is the tendency for a measurement system to measure lower or higher than the true value. In the lab findings in the Wells report, they indicate “the Exemplar Gauges underestimated the Master Gauge by an average of .07 psig”. This is an example of gage bias; the Exemplar gages measure .07 lower than true (page 20, note 20). This gage bias is small; however, what we will never know is the bias introduced by referees. Bias in a non-statistical sense infers intent, which is not part of the statistical interpretation of bias. In statistics, bias simply means the average tends to one side of the true value, without assuming malicious intent. I have no evidence, nor do I believe the referees had the intent to measure the footballs “low” or “high”. However, the measurement system can have bias regardless of intent. Many things can affect the bias, without the referees’ knowledge: how they hold the ball, the angle and depth of needle insertion, and how long they allow the readings to stabilize. If you look at the MSA data, you can see in the data that there is a bias between the two referees. Note that Appraiser 1 (referee 1) measures lower than Appraiser 2. For you stats people, the difference is statistically significant using a paired t-Test, but the difference isn’t normally distributed, violating one of the assumptions of the paired t-Test. However, there is another disturbing note in the data, which I’ve not had the time to analyze yet. The data below is the MSA data, but I’ve included a note of which team’s ball is being measured and the difference between the two referees.
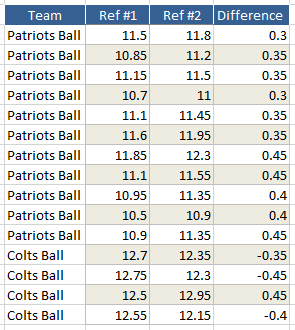
Again, the difference column is calculated as Ref #2- Ref #1. Note that the difference is positive for all of the Patriots’ balls, indicating that Ref #2 is biased higher than Ref #1. The disturbing part is that when they measure the Colts’ balls, three of the four differences are negative. I haven’t had time to do the math to determine if this is statistically significant or not, but I will in a future article. However, the main reason for this being disturbing is that Ref #2 measured three of the Colts balls out of spec (lower than 12.5). Had the tendency of Ref #1 to measure lower than Ref #2 continued (as you would expect) then Ref #1 would have measured all four of those balls less than 12.5. Had that occurred, this discussion would be around how BOTH teams had balls less than the required 12.5 psi. Again, it is possible this is random variation or that the referees swapped gages; I will do the formal math in a future article.
Given the difference between referees, the uncertainty in the bias from true, and the strange measurements coming from the data, my personal conclusion is that there isn’t sufficient confidence in the measurement system to conclude anything about the pressure of the balls on game day.
Final Note: At the time of this writing, I am not being paid by nor have I ever contacted or been contacted by anyone in the Patriots’ organization or the NFL.


Excellent, what a web site it is! This website presents helpful data to us, keep it up.
You actually make it appear so easy together with your presentation but I to find this topic to be actually one thing which I think I would never understand. It sort of feels too complex and very vast for me. I’m having a look forward to your subsequent put up, I will try to get the cling of it!
Good post. I will be experiencing some of these issues as well..
Thanks for every other informative blog. The place else may just I get that kind of info written in such an ideal means? I’ve a undertaking that I am simply now operating on, and I’ve been on the look out for such info.
I read this article completely about the comparison of latest and preceding technologies, it’s amazing article.